Introduction to Adjacency List for Graph

Graphs are an important data structure in computer science and are widely used to represent real-world relationships between objects. In this blog, we will be introducing a common way of representing graphs, known as an adjacency list.

Introduction

An Adjacency list is a collection of nodes that have an edge over each other. The advantage of this list over a regular graph is that you can edit or remove nodes from it easily. You can also add additional edges between two nodes if needed by using the add_edge method on your list object or calling another method (such as add_node()).

What is an Adjacency List?

It is a list that can be used to represent a graph. It is implemented as an array, with each element of the array representing a vertex in the graph. The elements of the array store the vertices that are adjacent to the vertex represented by the element. Each item contains two pieces of information:

• The first element of the array represents the number of neighbours (if any) surrounding it. While the second element holds its location in space, i.e., left/right/top/bottom etc.
• You may have noticed that there are some similarities between an adjacency list and a directed graph, where nodes connect only if they share an edge or have some kind of relationship with each other. However, unlike directed graphs where edges are always identified by numbers instead of text labels like A-B or 1->2->3->4->5. In contrast, undirected graphs don’t require such identification labels. Because all paths between two points are available simultaneously, without having any restrictions on how many paths could exist between them. Therefore, no restriction on how many paths exist.

Features of an Adjacency List 

Adjacency lists are a data structure that stores the relationship between vertices in a graph. The nodes in an adjacency list are referred to as vertices, and their neighbours are stored at the same level of abstraction (e.g., two adjacent vertices). They also allow you to add new edges or remove existing ones easily by simply adding or removing items from your list respectively.

Adjacent pairs are stored in sorted order so that you can easily find them when needed. This makes it easy for us to perform operations such as finding all paths between two vertices using their indices within these structures.

• An adjacency list only stores the edges of a graph, not the vertices, making it a space-efficient representation of a graph.
• It is also simple to implement and easy to modify.
• An adjacency list can be easily modified to store additional information about the edges in the graph, such as weights or labels.

Advantages of an Adjacency List

It is a data structure that stores the set of all vertices that are adjacent in a graph. It has several advantages over other graph structures such as adjacency lists being more efficient in terms of storage and access.

Adjacency lists can also be used to store and retrieve data. In addition, they can be used to implement algorithms on graphs. Like the shortest path or topological ordering which requires numeric values (the distance between two vertices).

Drawbacks of an Adjacency Lists

• Adjacency lists are one of the most common graphs. They have an O(n) time complexity, and they use memory to store their nodes.
• The size of an adjacency list is also very high. This means that if you want to store large amounts of data on your adjacency list. It will be slow because of the amount of memory used by each node in the graph.
• It is not efficient for finding the edges connecting a particular vertex. As we have to traverse the entire linked list to find the desired edge.
• Another disadvantage is that it is not easy to find the degree of a vertex in an adjacency list. As we have to count the number of edges in the corresponding linked list.

Graph representing Adjacency List

A graph is a collection of nodes and edges. Nodes are connected by edges, which can be directed or undirected. An edge is a connection between two nodes, where one node is called the source and the other one is called the target. Edges are often represented as lines on paper or screens, but they can also be visualized as arrows in space (e.g., in Google Earth).

An important concept to remember about graphs is that we can add more than one edge between two given vertices. Like this:

This means we have multiple paths connecting two vertices together. Also note that there may be multiple paths connecting two vertices if they share some common property (e.g., location).

Below is an example of a graph represented using an adjacency list:

Vertex 0: [1, 2]

Vertex 1: [0, 2]

The Vertex 2: [0, 1, 3]

And Vertex 3: [2]

In this example, the adjacency list for vertex 0 is [1, 2], which means that vertex 0 is connected to vertices 1 and 2. Similarly, the adjacency list for vertex 1 is [0, 2], which means that vertex 1 is connected to vertices 0 and 2.

Example of an Adjacency List

Consider the following graph:

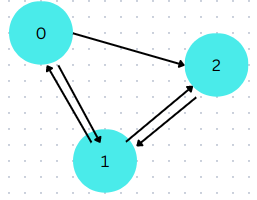
To represent this graph as list:

Vertex 0: [1, 2]

Vertex 1: [0, 2]

and Vertex 2: [1]

Implementation of an Adjacency List

This can be implemented in several ways, such as using an array of linked lists or an array of sets. Below is an example of its implementation using an array of linked lists in Python:

class Graph:
  def __init__(self, num_vertices):
    self.num_vertices = num_vertices
    self.adjacency_list = [[] for _ in range(num_vertices)]
    
  def add_edge(self, v1, v2):
    self.adjacency_list[v1].append(v2)
    self.adjacency_list[v2].append(v1)
    
  def print_graph(self):
    for i, vertex in enumerate(self.adjacency_list):
      print(f"Vertex {i}: {vertex}")
      
g = Graph(4)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 3)
g.print_graph()
Code language: Python (python)

The above code creates a graph with 4 vertices and 4 edges and adds the edges to the adjacency list using the add_edge function. The print_graph function is then used to print the adjacency list. The output of this code will be:

Vertex 0: [1, 2]
Vertex 1: [0, 2]
Vertex 2: [0, 1, 3]
Vertex 3: [2]
Code language: Python (python)

Conclusion

In summary, These lists are a simple and space-efficient way of representing a graph and are easy to modify and implement. However, it has some drawbacks, such as inefficiency in finding the edges of a particular vertex and difficulty in finding the degree of a vertex. It is important to choose the appropriate representation of a graph depending on the specific needs of the application.

FAQs

What is an adjacency list example?

It is a data structure that is used to represent a finite graph. It is a list of lists, where each list represents a vertex in the graph and contains the vertices that are adjacent to it.

Such as, consider the following graph:

How do you represent an adjacency list?

Representation of the adjacency list shown in the above graph would be:

10 -> 20 -> 40
20 -> 10 -> 30
30 -> 20 -> 40
40 -> 10 -> 30
Code language: Python (python)

What is an adjacency list in C++?

To represent this in C++, you can use an array of linked lists.

#include <iostream>
#include <list>

using namespace std;

const int N = 5;

int main() {
  list<int> adjacency_list[N];

  adjacency_list[1].push_back(2);
  adjacency_list[1].push_back(4);
  adjacency_list[2].push_back(1);
  adjacency_list[2].push_back(3);
  adjacency_list[3].push_back(2);
  adjacency_list[3].push_back(4);
  adjacency_list[4].push_back(1);
  adjacency_list[4].push_back(3);

  return 0;
}
Code language: C++ (cpp)

Is an adjacency list an array?

No, It is a list of lists, not an array. It is an efficient representation of a graph when the graph is sparse. That is when it has a small number of edges compared to the number of vertices.

What are the advantages and disadvantages of an adjacency list?

There are several advantages of using it, to represent a graph. First, it is easy to implement and requires only a small amount of memory. Second, it allows for efficient insertion and deletion of edges. Finally, it can be used to represent both directed and undirected graphs.

There are also some disadvantages to using it. First, it can be slower than other representations. Such as an adjacency matrix, when it comes to querying the graph. Second, it is not well-suited for dense graphs, that is, graphs with a large number of edges. Finally, it can be more difficult to implement some graph algorithms using an adjacency list compared to other representations.